Lectura y construcción de gráficas formadas por secciones rectas y curvas

Lectura y construcción de gráficas de funciones cuadráticas

Semejanza en la construcción de figuras Homotéticas.

Definición

Homotecia es la transformación geométrica de una figura plana en otra figura de igual forma, pero de menor o mayor tamaño. 
Dicho tamaño depende, según el valor de la razón de homotecia (k). 
Si k es positivo la homotecia es directa, y si es negativo, entonces la homotecia es inversa.

Tipos de homotecias

1) Homotecia directa : Es una homotecia con centro en el punto O y razón de homotecia k > 0  (positiva).
Es este caso el centro de homotecia (O) esta frente o detrás de las figuras homotéticas (A y A').  Es decir, A y A′ están al mismo lado de O.

 2) Homotecia inversa:  Es una homotecia con centro en el punto O y razón de homotecia k < 0  (negativa).

Y para este caso el centro de homotecia (O) esta en medio de las figuras homotéticas (A y A').  

Ejercicios Resueltos

1. Si  K = 2, dibuja el triángulo semejante al original ABC, partiendo del centro "O".

Solucion:  Como K = 2  entonces multiplicamos ese valor por la distancia que hay del centro O hasta A para obtener el segmento OA', es decir: 
K · OA = OA'    y hacemos lo mismo para encontrar las distancias OB' y OC' , es decir 
K · OB = OB' 
K · OB = OC'
Y por lo tanto la figura que obtendremos sera la siguiente
2. Disminuye la siguiente figura sabiendo que K = 1/2, y partiendo del origen "O".


Solucion:  Para encontrar la figura homotetica (A'B'C'D')  basta saber la distancia que hay de O hasta A, B, C y D respectivamente. Posteriormente multiplicamos esas dimensiones por K, es decir:

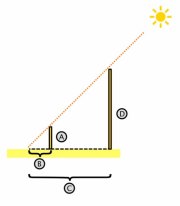
3. En la siguiente figura ¿Que altura tiene el árbol?

A continuación te invito a dar click a los siguientes links donde podrás tener acceso a contenido multimedia para ahondar y reafirmar tus aprendizajes sobre figuras semejantes y Homotecia.

https://www.youtube.com/watch?v=zlUlG2KP7vI

https://www.youtube.com/watch?v=75n2BKVO8p4

Homotecia en la vida cotidiana.

¿Cuándo fue la última vez que fuiste a un cine? Te das cuenta del gran tamaño de las imágenes en pantalla, ¿cómo se logra?

En las salas de cine se cuenta con un proyector de imágenes especial, que usa una potente lámpara como fuente de luz y la película en forma de cinta delgada. El proceso es sencillo, en su base, la fuente de luz pasa por la cinta y proyectan imágenes pequeñas a gran tamaño en la pantalla del cine.

Esto implica, que cuando se construye la sala de cine, se deben hacer los cálculos necesarios para tener la certeza de que el tamaño de la imagen proyectada será del justo tamaño de la pantalla situada al frente de la sala, de otra forma podría proyectarse una imagen demasiado grande o pequeña lo que afectaría su claridad.

Las pantallas de cine más grandes llegan a medir entre 20m por 28m y 22m por 16m, aunque no hay un  estándar, pueden ser incluso mayores.

Si tienes ganas de experimentar con esta forma en que se comportan las figuras proyectadas usando el principio de homotecia, puedes visitar la siguiente página de internet, donde se encuentra un divertido simulador que puedes manipular, el enlace es el siguiente:

http://descartes.cnice.mec.es/materiales_didacticos/Semejanza_y_homotecia/Homote1.htm

Teorema de Thales

Breve reseña histórica

Tales (o Thales) de Mileto, además de comerciante, científico y estadista, fue un sabio filósofo y matemático griego que vivió entre los siglos VI y V aC. Aunque no se conoce mucho sobre su vida, ya desde los tiempos de Platón su figura aparece enmarcada en la leyenda. 

Un hecho cierto es que apenas se tiene constancia clara acerca de sus escritos. Por ejemplo, el conocimiento de la filosofía de Tales  y su escuela de Mileto, de la que fue fundador, se debe a Aristóteles.

Algunos autores han dicho de Tales que adquirió parte de sus conocimientos de los sacerdotes durante un viaje que realizó siendo todavía joven a Egipto. Allí fue donde puso en práctica sus logros en matemáticas, en especial en geometría, áreas en las que luego hizo descubrimientos fundamentales. Aunque muchos libros le atribuyen hasta cinco teoremas de geometría elemental, existen evidencias de solo dos:

Primer Teorema

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes (es decir, sus ángulos correspondientes son iguales y sus lados son proporcionales entre si).

Este teorema recoge uno de los principios básicos de la geometría, siendo su principal aplicación, y la razón de su fama, el establecimiento de la condición de semejanza de triángulos, de la cual se obtiene el siguiente corolario:

“Si dos triángulos son semejantes sus lados son proporcionales”.
O lo que es lo mismo, la razón entre la longitud de dos de ellos se mantiene constante en el otro. 

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente. Según Herodoto, el propio Tales empleó este corolario para medir en Egipto la altura de la pirámide de Keops. 

En cualquier caso, el teorema demuestra la semejanza entre dos triángulos, no la constancia del cociente.

Segundo Teorema

Se trata de un teorema de geometría enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos. Su enunciado es el siguiente:

Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. El triángulo ABC resulta ser un triángulo rectángulo.

Aunque se acepta por haber sostenido en su época lo que expresa el teorema, no existe constancia histórica de su atribución.

Otros teoremas también atribuidos a Tales, algunos con dudas porque no quedó nada escrito, son:
– Cualquier diámetro de un círculo lo divide en dos partes iguales.
– Los ángulos entre dos líneas rectas que se cortan son iguales.
– Los ángulos de la base de un triángulo isósceles son iguales.

Tales fue el primero y más famoso de los Siete Sabios de Grecia, título dado por la tradición griega a un grupo de sabios que incluye a filósofos, estadistas o legisladores, y que se mantuvo a lo largo de los siglos. Para terminar, que mejor que una anécdota de Tales en su faceta de astrónomo contada por Platón:

“Una noche Tales estaba observando el cielo, más de repente tropezó y se cayó. Uno de sus sirvientes le levantó presto y le dijo: 

“Cómo pretendes entender lo que pasa en el cielo, si no puedes ver lo que se encuentra a tus pies en la tierra”.

Teorema de Tales en rectas paralelas y secantes

Si dos rectas cualesquiera ("r" y "s") se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

     

Ejemplos

1 Las rectas a, b y c son paralelas. Halla la longitud de x.

2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

3/2 = 6/4 = 1.5 (proporción o escala entre segmentos correspondientes)

Teorema de Tales en un triangulo

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo A'B'C', cuyos lados son proporcionales a los del triángulo ABC.

     

Ejemplo:

Hallar las medidas de los segmentos a y b.

Aplicaciones del Teorema de Tales

Ejercicios complementarios

A continuación te invito a dar click a los siguientes links donde podrás tener acceso a contenido multimedia para ahondar y reafirmar tus aprendizajes sobre el Teorema de Tales y sus aplicaciones.

https://www.youtube.com/watch?v=e2SDoARhAwg

https://www.youtube.com/watch?v=e_MvZr2sNmo

Regla del producto en Probabilidad para eventos independientes

Definiciones

Eventos independientes

Dos eventos son independientes si el resultado del segundo evento no es afectado por el resultado del primer evento. 

Es decir, son aquellos eventos cuyo resultado no tienen que ver con el resultado de otro(s) evento(s).

Por ejemplo, el resultado de lanzar una moneda, y que caiga de cualquier lado, no depende del resultado de ninguno de los lanzamientos anteriores. Por lo tanto, cada lanzamiento es un evento independiente

Regla del producto:

Por lo anterior, Si A y B son eventos independientes, la probabilidad de que ambos eventos ocurran es el producto de las probabilidades de los eventos individuales.

         P(A y B) = P(A) · P(B)

Ejemplo 1:

Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y luego reemplazada. Otra canica se saca de la caja. 

¿Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?

Solución:

Ya que la primera canica es reemplazada (es decir se saca y se vuelve a meter la misma canica u otra del mismo color), el tamaño del espacio muestral (9) no cambia de la primera sacada a la segunda, así los eventos son independientes.

P(azul luego verde) = P(azul) · P(verde)

                             

Otros ejemplos ilustrativos

1) De una baraja estándar de 52 cartas sea A el suceso de sacar un As en la primera extracción y B sacar un Rey en la segunda extracción. Calcular la probabilidad de sacar un As y un Rey en dos extracciones devolviendo la carta extraída.

Solución:

A y B son sucesos independientes porque la ocurrencia de A afecta la probabilidad de ocurrencia de B.

La probabilidad de que la primera carta sea un As es:

Reemplazando los anteriores valores en la regla particular de la multiplicación se obtiene:

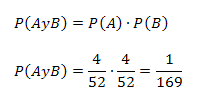
2) Una pareja de esposos desean tener 3 hijos. Suponiendo que las probabilidades de tener un niño o una niña son iguales, calcular la probabilidad de éxito en tener hombre en el primer nacimiento, mujer en el segundo nacimiento y hombre en el tercer nacimiento.

Solución:

M = mujer

H = hombre

Elaborando un diagrama de árbol se tiene todas las probabilidades:

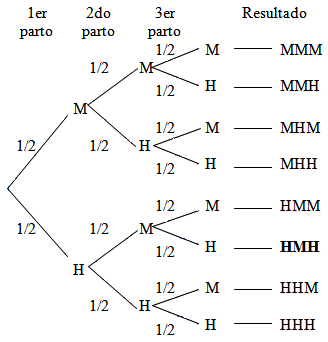
Entonces,

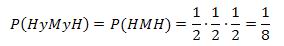
Ahora te invito a que des click en el siguiente enlace para acceder a mas información y ejemplos sobre regla del producto para eventos independientes.


https://www.youtube.com/watch?v=G-TUFDK8jOU

https://www.youtube.com/watch?v=JyBGhhGY4o4

Desviación media y Rango de un conjunto de datos estadísticos.

Las medidas de dispersión (como la desviación media y el Rango), también llamadas de variabilidad, nos informan sobre cuánto se alejan del centro (media aritmética) los valores de un conjunto de datos.

Cuanto más alejados del centro, mayor será la variabilidad, lo cual en términos prácticos indica que los datos están muy alejados entre sí (muy dispersos).

Por el contrario entre más cerca del centro estén, significa que los datos están muy cercanos entre sí. 

Cuando una distribución de datos tiene poca dispersión toma el nombre de distribución homogénea y si su dispersión es alta se llama heterogénea.

Desviación media

También se le conoce como desviación media absoluta. Es la media aritmética de los valores absolutos de las desviaciones. (Y dichas desviaciones son el resultado de restar cada valor respecto a la media).

La desviación media se calcula con la formula:

Ejemplo:  Calcular la desviación media para los siguientes datos:

2, 9, 10, 2, 3, 1,9,9,1,4

a)   Calculamos el promedio y obtenemos que es igual a 5.

b)   Se obtiene el valor absoluto de la diferencia de cada dato y el promedio y se suman los resultados, es decir: 

c)  Finalmente, el resultado anterior (34)  se divide entre 10, así la desviación media (DM) de los datos es 3.4

Ahora te invito a que des click en el siguiente enlace para acceder a mas información y ejemplos sobre desviación media y rango.

https://www.youtube.com/watch?v=IppiARlHhzo
https://www.youtube.com/watch?v=Sqk8NVK3J-o

Solución de ecuaciones cuadráticas por medio de la formula general

Recordemos que una ecuación cuadrática, es una expresión algebraica que sigue la siguiente estructura:

En tal ecuación a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.

La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes

Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente más grande es un cuadrado (en otras palabras x2).

Ejemplos de ecuaciones cuadráticas:

		En esta a=2, b=5 y c=3
		Aquí hay una un poco más complicada: ¿Dónde está a? En realidad a=1, porque normalmente no escribimos "1x2" b=-3 ¿Y dónde está c? Bueno, c=0, así que no se ve.
		¡Ups! Esta no es una ecuación cuadrática, porque le falta el x2 (es decir a=0, y por eso no puede ser cuadrática)

¿Qué tienen de especial?

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:

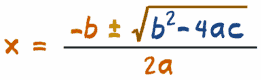
	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!
	La parte azul (b2 - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios .

Solución aplicando la formula general

Para resolver una ecuación cuadrática o de segundo grado, sólo substituye los valores de a,b y c en la fórmula cuadrática y haz los cálculos.

Ejemplo: resuelve 5x² + 6x + 1 = 0

Recuerda, la fórmula general cuadrática es:  x = [ -b ± √(b²-4ac) ] / 2a

Y por otro lado, los coeficientes en la ecuación:  a = 5, b = 6, c = 1

Ahora sustituye a,b,c en la formula y tenemos: x = [ -6 ± √(6²-4×5×1) ] / 2×5

Resolviendo operaciones: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10

Y entonces tenemos como respuesta: x1 = -0.2  y x2 = -1

Comprobación:
5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0.

Ecuaciones cuadráticas disfrazadas

Algunas ecuaciones no parece que sean cuadráticas, pero con manipulaciones astutas se pueden transformar en una:

Disfrazadas	Qué hacer	En forma estándar	a, b y c
x2 = 3x -1	Mueve todos los términos a la izquierda	x2 - 3x + 1 = 0	a=1, b=-3, c=1
2(x2 - 2x) = 5	Desarrolla paréntesis	2x2 - 4x - 5 = 0	a=2, b=-4, c=-5
x(x-1) = 3	Desarrolla paréntesis	x2 - x - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x2 = 0	Multiplica por x2	5x2 + x - 1 = 0	a=5, b=1, c=-1

Otro ejemplo resuelto: Encontrar las raíces para  2x² + 3x − 5 = 0

Vemos claramente que a = 2,     b = 3   y     c = −5, así es que:

Ahora, tenemos que obtener las dos soluciones, con el + y con el − :

  y también      

Así es que las soluciones son .

Ahora te invito a que des click en el siguiente enlace para acceder a mas información y ejemplos sobre solución de ecuaciones cuadráticas por formula general.
https://www.youtube.com/watch?v=sdWh5CnYIX4
http://conteni2.educarex.es/mats/11979/contenido/
Nota: A veces las paginas tardan un poquito en abrir...ten paciencia...te aseguro que vale la pena.!