Teorema de Thales

Breve reseña histórica

Tales (o Thales) de Mileto, además de comerciante, científico y estadista, fue un sabio filósofo y matemático griego que vivió entre los siglos VI y V aC. Aunque no se conoce mucho sobre su vida, ya desde los tiempos de Platón su figura aparece enmarcada en la leyenda. 

Un hecho cierto es que apenas se tiene constancia clara acerca de sus escritos. Por ejemplo, el conocimiento de la filosofía de Tales  y su escuela de Mileto, de la que fue fundador, se debe a Aristóteles.

Algunos autores han dicho de Tales que adquirió parte de sus conocimientos de los sacerdotes durante un viaje que realizó siendo todavía joven a Egipto. Allí fue donde puso en práctica sus logros en matemáticas, en especial en geometría, áreas en las que luego hizo descubrimientos fundamentales. Aunque muchos libros le atribuyen hasta cinco teoremas de geometría elemental, existen evidencias de solo dos:

Primer Teorema

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes (es decir, sus ángulos correspondientes son iguales y sus lados son proporcionales entre si).

Este teorema recoge uno de los principios básicos de la geometría, siendo su principal aplicación, y la razón de su fama, el establecimiento de la condición de semejanza de triángulos, de la cual se obtiene el siguiente corolario:

“Si dos triángulos son semejantes sus lados son proporcionales”.
O lo que es lo mismo, la razón entre la longitud de dos de ellos se mantiene constante en el otro. 

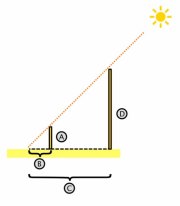
Este corolario es la base de la geometría descriptiva. Su utilidad es evidente. Según Herodoto, el propio Tales empleó este corolario para medir en Egipto la altura de la pirámide de Keops. 

En cualquier caso, el teorema demuestra la semejanza entre dos triángulos, no la constancia del cociente.

Segundo Teorema

Se trata de un teorema de geometría enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos. Su enunciado es el siguiente:

Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. El triángulo ABC resulta ser un triángulo rectángulo.

Aunque se acepta por haber sostenido en su época lo que expresa el teorema, no existe constancia histórica de su atribución.

Otros teoremas también atribuidos a Tales, algunos con dudas porque no quedó nada escrito, son:
– Cualquier diámetro de un círculo lo divide en dos partes iguales.
– Los ángulos entre dos líneas rectas que se cortan son iguales.
– Los ángulos de la base de un triángulo isósceles son iguales.

Tales fue el primero y más famoso de los Siete Sabios de Grecia, título dado por la tradición griega a un grupo de sabios que incluye a filósofos, estadistas o legisladores, y que se mantuvo a lo largo de los siglos. Para terminar, que mejor que una anécdota de Tales en su faceta de astrónomo contada por Platón:

“Una noche Tales estaba observando el cielo, más de repente tropezó y se cayó. Uno de sus sirvientes le levantó presto y le dijo: 

“Cómo pretendes entender lo que pasa en el cielo, si no puedes ver lo que se encuentra a tus pies en la tierra”.

Teorema de Tales en rectas paralelas y secantes

Si dos rectas cualesquiera ("r" y "s") se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

     

Ejemplos

1 Las rectas a, b y c son paralelas. Halla la longitud de x.

2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

3/2 = 6/4 = 1.5 (proporción o escala entre segmentos correspondientes)

Teorema de Tales en un triangulo

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo A'B'C', cuyos lados son proporcionales a los del triángulo ABC.

     

Ejemplo:

Hallar las medidas de los segmentos a y b.

Aplicaciones del Teorema de Tales

Ejercicios complementarios

A continuación te invito a dar click a los siguientes links donde podrás tener acceso a contenido multimedia para ahondar y reafirmar tus aprendizajes sobre el Teorema de Tales y sus aplicaciones.

https://www.youtube.com/watch?v=e2SDoARhAwg

https://www.youtube.com/watch?v=e_MvZr2sNmo